จากตอนที่แล้วที่แล้วผู้เขียนได้กล่าวถึง Linear Regression (Univariate) โดยมีเพียง feature (x x x f ( x ) = w x + b f(x) = wx+b f ( x ) = w x + b
แล้วถ้าต้องใช้หลาย features ตัว Linear Regression model จะมีหน้าตาเป็นยังไงล่ะ?
Linear Regression Model (with variate) f w , b ( x ) = w 1 x 1 + w 2 x 2 + . . . + w n x n + b f_{w,b}(x) = w_1x_1+w_2x_2+...+w_nx_n+b f w , b ( x ) = w 1 x 1 + w 2 x 2 + ... + w n x n + b หรือ
f w , b = ∑ j = 1 n w j x j + b \begin{equation}
f_{w,b} = \sum _{j=1} ^n w_jx_j+b
\end{equation} f w , b = j = 1 ∑ n w j x j + b แค่นี้?
ใช่แค่นี้จริงๆ
เราสามารถเขียนให้อยู่ในรูปแบบของ vector (Vectorization)ได้ดังนี้
w ⃗ = [ w 1 , w 2 , w 3 , . . . , w n ] x ⃗ = [ x 1 , x 2 , x 3 , . . . , x n ] \begin{aligned}
\vec {w} &= [w_1,w_2,w_3,...,w_n]\\
\vec {x} &= [x_1,x_2,x_3,...,x_n]
\end{aligned} w x = [ w 1 , w 2 , w 3 , ... , w n ] = [ x 1 , x 2 , x 3 , ... , x n ] f w ⃗ , b = w ⃗ ⋅ x ⃗ + b \begin{equation}
f_{\vec{w},b} = \vec{w}\cdot\vec{x} + b\\
\end{equation} f w , b = w ⋅ x + b ในการ implement code การ implement โดยใช้ฟังก์ชัน dot product ของ NumPy จะใช้เวลาน้อยกว่าเนื่องจาก NumPy ได้ implement dot product ให้มีการคำนวณแบบขนาน
💡
Playground
ข้างล่างเป็นตัวอย่างcodeที่เปรียบเทียบการใช้เวลาในการทำ dot product ที่เรา implement เองกับ method ของ NumPy
import numpy as np
import time
def loop_dot(a, b):
"""
implement ตามสมการที่ 1
a : input vector
b : input vector ที่มี dimension เท่า a
Returns:
x : ผลลัพธ์สุดท้าย
"""
x=0
for i in range(a.shape[0]):
x = x + a[i] * b[i]
return x
# สร้าง narray แบบสุ่มขนาด 10000000 ตัว
np.random.seed(1)
a = np.random.rand(10000000)
b = np.random.rand(10000000)
start = time.time()
c = np.dot(a, b)
end = time.time()
print(f"np.dot(a, b) = {c:.4f}")
print(f"Vectorized version duration: {1000*(start-end):.4f} ms ")
start = time.time()
c = loop_dot(a,b)
end = time.time()
print(f"loop_dot(a, b) = {c:.4f}")
print(f"loop version duration: {1000*(start-end):.4f} ms ")
เราได้เห็นถึงประโยชน์ของการทำ Vectorization ไปแล้วนอกจากจะทำให้การคำนวณเร็วขึ้นแล้วผู้เขียนเองยังมองว่าเมื่อเขียนเป็นสมการในรูปแบบของ vector แล้วทำให้อ่านได้สบายตากว่าด้วย(?) ต่อไปเรามาเปลี่ยนสมการที่อยู่ในตอนที่ 1 ให้อยู๋ในรูปแบบ vectorized กัน
w 1 , … , w n b w_1,…,w_n \\
b w 1 , … , w n b w ⃗ = [ w 1 , … , w n ] b \vec {w} = [w_1,…,w_n] \\
b w = [ w 1 , … , w n ] b f w , b ( x ) = w 1 x 1 + . . . + w n x n + b f_{w,b}(x) = w_1x_1+...+w_nx_n+b f w , b ( x ) = w 1 x 1 + ... + w n x n + b f w ⃗ , b ( x ⃗ ) = w ⃗ ⋅ x ⃗ + b f_{\vec{w},b} (\vec x) = \vec{w}\cdot\vec{x} + b f w , b ( x ) = w ⋅ x + b J ( w 1 , … , w n , b ) J(w_1,…,w_n,b) J ( w 1 , … , w n , b ) J ( w ⃗ , b ) J(\vec w,b) J ( w , b ) R e p e a t { w n e w = w o l d − α ∂ ∂ w J ( w 1 , … , w n , b ) b n e w = b o l d − α ∂ ∂ b J ( w 1 , … , w n , b ) } Repeat\{\\
w_{new} = w_{old}-\alpha \frac{\partial}{\partial w}J(w_1,…,w_n,b) \\
b_{new} = b_{old}-\alpha \frac{\partial}{\partial b}J(w_1,…,w_n,b)\\\}
R e p e a t { w n e w = w o l d − α ∂ w ∂ J ( w 1 , … , w n , b ) b n e w = b o l d − α ∂ b ∂ J ( w 1 , … , w n , b ) }
R e p e a t { w n e w j = w o l d j − α ∂ ∂ w J ( w ⃗ , b ) b n e w = b o l d − α ∂ ∂ b J ( w ⃗ , b ) } Repeat\{\\
w_{new_j} = w_{old_j}-\alpha \frac{\partial}{\partial w}J(\vec w,b) \\
b_{new} = b_{old}-\alpha \frac{\partial}{\partial b}J(\vec w,b)\\\} R e p e a t { w n e w j = w o l d j − α ∂ w ∂ J ( w , b ) b n e w = b o l d − α ∂ b ∂ J ( w , b ) }
ขอลงลายละเอียดในส่วน loop ของ Gradient Descent สักหน่อย
R e p e a t u n t i l c o n v e r g e n c e { w j n e w = w j o l d − α ∂ ∂ w J ( w ⃗ , b ) b n e w = b o l d − α ∂ ∂ b J ( w ⃗ , b ) } \begin{aligned}
&Repeat\,until\,convergence\{\\
&w_{j_{new}} = w_{j_{old}}-\alpha \frac{\partial}{\partial w}J(\vec w,b) \\
&b_{new} = b_{old}-\alpha \frac{\partial}{\partial b}J(\vec w,b)\\
&\}
\end{aligned} R e p e a t u n t i l co n v er g e n ce { w j n e w = w j o l d − α ∂ w ∂ J ( w , b ) b n e w = b o l d − α ∂ b ∂ J ( w , b ) } จากที่เราทำ Partial Derivative Cost function ไปในตอนที่ 1 จะสามารถเขียนให้อยู่ในรูปแบบนี้
R e p e a t u n t i l c o n v e r g e n c e { w j n e w = w j o l d − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x 1 ( i ) b n e w = b o l d − α 1 m ∑ i = 1 m ( w x ( i ) + b − y ( i ) ) } \begin{aligned}
&Repeat\,until\,convergence\{\\
&w_{j_{new}} = w_{j_{old}}-\alpha\frac{1}{m}\sum_{i=1}^m(f_{\vec w,b}(\vec x^{(i)})-y^{(i)})x_1^{(i)}\\
&b_{new} = b_{old}-\alpha\frac{1}{m}\sum_{i=1}^m(wx^{(i)}+b-y^{(i)})\\
&\}
\end{aligned} R e p e a t u n t i l co n v er g e n ce { w j n e w = w j o l d − α m 1 i = 1 ∑ m ( f w , b ( x ( i ) ) − y ( i ) ) x 1 ( i ) b n e w = b o l d − α m 1 i = 1 ∑ m ( w x ( i ) + b − y ( i ) ) } w j w_j w j
R e p e a t u n t i l c o n v e r g e n c e { w 1 n e w = w 1 o l d − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x 1 ( i ) . . . w n n e w = w n o l d − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) x n ( i ) b n e w = b o l d − α 1 m ∑ i = 1 m ( w x ( i ) + b − y ( i ) ) } \begin{aligned}
&Repeat\,until\,convergence\{\\
&w_{1_{new}} = w_{1_{old}}-\alpha\frac{1}{m}\sum_{i=1}^m(f_{\vec w,b}(\vec x^{(i)})-y^{(i)})x_1^{(i)}\\
.\\.\\.\\
&w_{n_{new}} = w_{n_{old}}-\alpha\frac{1}{m}\sum_{i=1}^m(f_{\vec w,b}(\vec x^{(i)})-y^{(i)})x_n^{(i)}\\
&b_{new} = b_{old}-\alpha\frac{1}{m}\sum_{i=1}^m(wx^{(i)}+b-y^{(i)})\\
&\}
\end{aligned} . . . R e p e a t u n t i l co n v er g e n ce { w 1 n e w = w 1 o l d − α m 1 i = 1 ∑ m ( f w , b ( x ( i ) ) − y ( i ) ) x 1 ( i ) w n n e w = w n o l d − α m 1 i = 1 ∑ m ( f w , b ( x ( i ) ) − y ( i ) ) x n ( i ) b n e w = b o l d − α m 1 i = 1 ∑ m ( w x ( i ) + b − y ( i ) ) } 💡
ทางเลือกอื่นสำหรับ Gradient Descent
Normal Equation ข้อดี
ใช้สำหรับ Linear Equation เท่านั้น สามารถหาค่า w, b ได้โดยไม่ต้องมีการทำซ้ำ ข้อเสีย
ไม่ได้ครอบคลุม Learning Algorithm อื่นๆ ถ้า features มีจำนวนมากจะช้า ใน Library ที่มีการ implement Linear Regression อาจจะมีการใช้วิธีการนี้ใน back-end
มาพูดถึง Feature ที่เป็นตัวเอกของตอนนี้กันดีกว่า ในกรณีที่มีหลาย features และแต่ละ feature ก็จะมีลักษณะที่แตกต่างกันออกไป เช่น ช่วงของค่าแต่ละ feature อาจมีช่วงที่กว้าง หรือ แคบก็ได้ ฯลฯ และเมื่อนำไปใส่ใน Gradient Descent การก้าวแต่ละก้าวอาจทำให้เกิดผลกระทบที่ใหญ่มากกับ feature บางตัวได้ ตอนนี้อาจจะยังงงๆ เราจะค่อยๆไปกัน
ตัวอย่างการทำนายราคาบ้าน
กำหนดให้
Regression model :
ขนาด (ฟุต2 ^2 2
จำนวนห้องนอน :
ช่วง [0-5]
p r i c e ^ = w 1 x 1 + w 2 x 2 + b \hat {price} = w_1x_1+w_2x_2+b
p r i ce ^ = w 1 x 1 + w 2 x 2 + b
x 1 x_1 x 1
x 2 x_2 x 2
บ้านขนาด 2000 ตารางฟุต มีห้องนอน 5 ห้อง ราคา 500k
กรณี 1
ถ้าเรากำหนดให้ w 1 = 50 , w 2 = 0.1 , b = 50 w_1 = 50,w_2 = 0.1, b = 50 w 1 = 50 , w 2 = 0.1 , b = 50
p r i c e ^ = ( 50 ) ( 2000 ) + ( 0.1 ) ( 5 ) + 50 p r i c e ^ = 100 , 050.5 k \begin{aligned}
\hat {price} &= (50)(2000) + (0.1)(5) + 50 \\
\hat {price} &= 100,050.5k
\end{aligned} p r i ce ^ p r i ce ^ = ( 50 ) ( 2000 ) + ( 0.1 ) ( 5 ) + 50 = 100 , 050.5 k กรณี 2
ถ้าเรากำหนดให้ w 1 = 0.1 , w 2 = 50 , b = 50 w_1 = 0.1,w_2 = 50, b = 50 w 1 = 0.1 , w 2 = 50 , b = 50
p r i c e ^ = ( 0.1 ) ( 2000 ) + ( 50 ) ( 5 ) + 50 p r i c e ^ = 500 k \begin{aligned}
\hat {price} &= (0.1)(2000) + (50)(5) + 50 \\
\hat {price} &= 500k\end{aligned} p r i ce ^ p r i ce ^ = ( 0.1 ) ( 2000 ) + ( 50 ) ( 5 ) + 50 = 500 k ในกรณีที่ 2 ราคาบ้านที่ได้ออกมามีความสมเหตุสมผลมากว่ากรณีที่ 1
จากทั้ง 2 กรณีจะสังเกตได้ว่าถ้าหากช่วง(range)ของ feature มีขนาดกว้างจะส่งผลดีกว่าถ้าเลือก weight ที่มีขนาดเล็ก และถ้ามีขนาดแคบจะส่งผลดีกว่าถ้าเลือก weight ที่มีขนาดใหญ่
แล้วมันเกี่ยวอะไรกับ Gradient Descent ล่ะ?
ตารางแสดงการเปรียบเทียบระหว่างขนาดของ Features และ Parameters
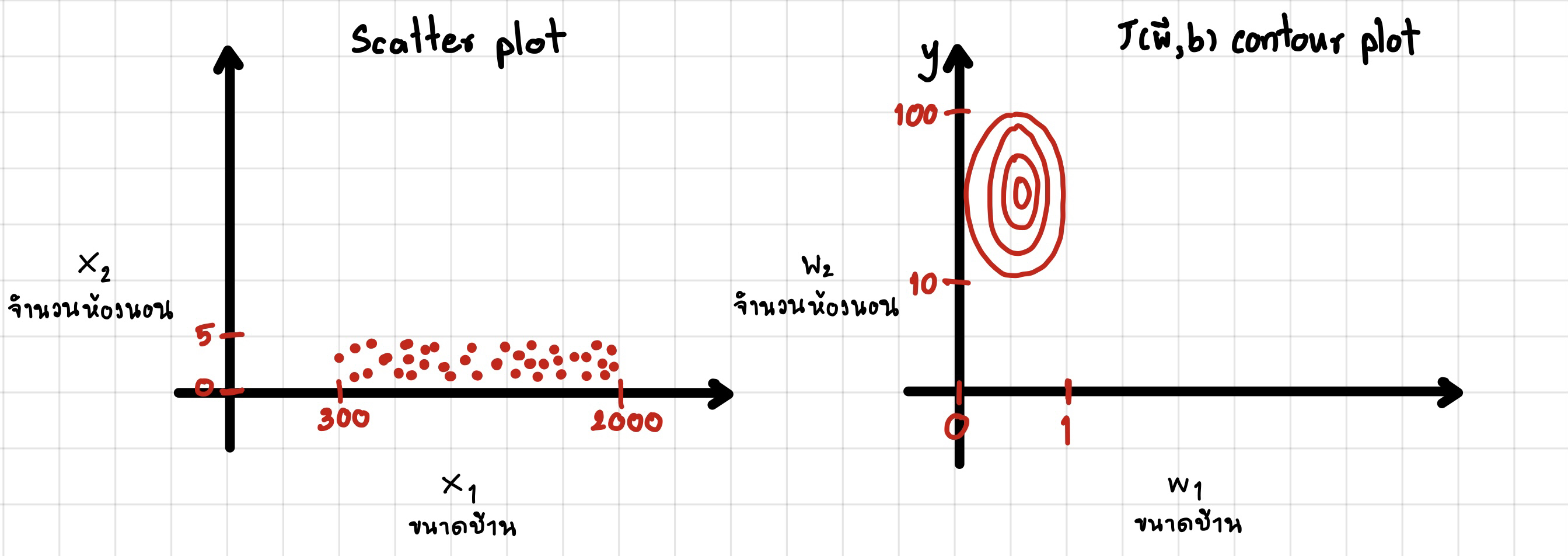
รูปซ้ายมือคือ scatter plot ของชุดข้อมูล
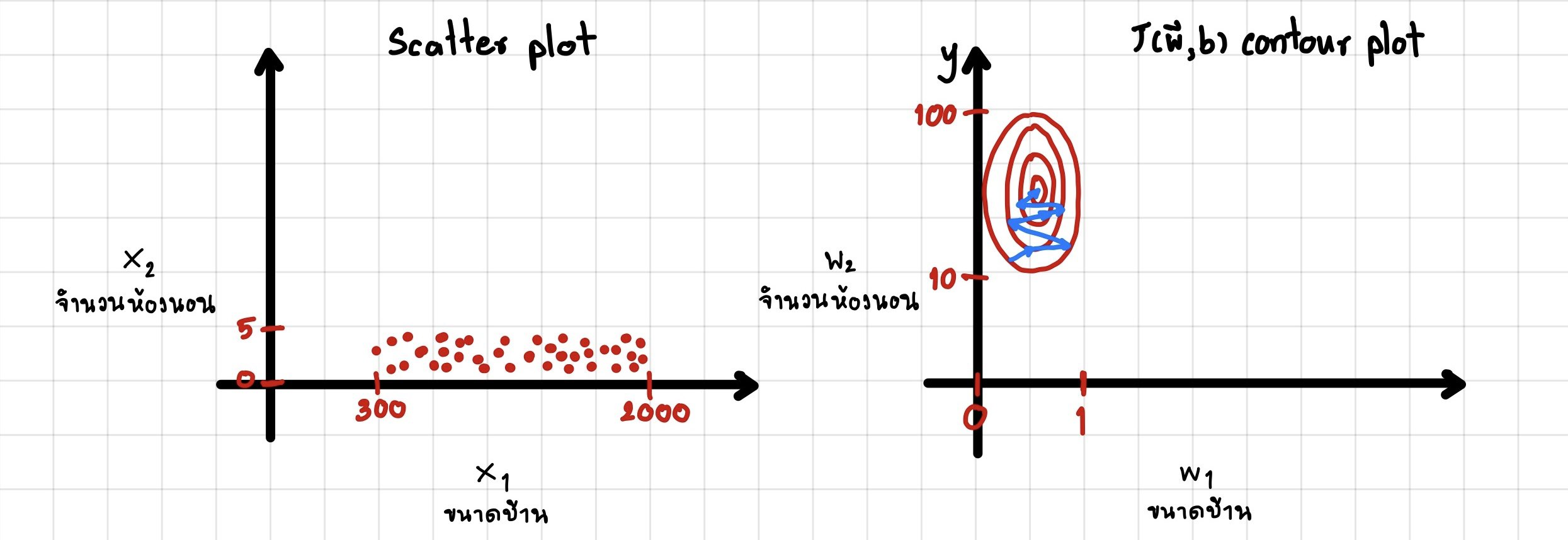
รูปขวามือคือ กราฟ cost function ระหว่าง w 1 , w 2 w1,w2 w 1 , w 2 สังเกตดูว่า Contour plot จะมีรูปร่างที่ผอม เมื่อเรานำไปใส่ Gradient Descent อาจใช้เวลานานในการหาจุดต่ำสุด(เส้นสีฟ้้า) ดังรูปข้างล่าง
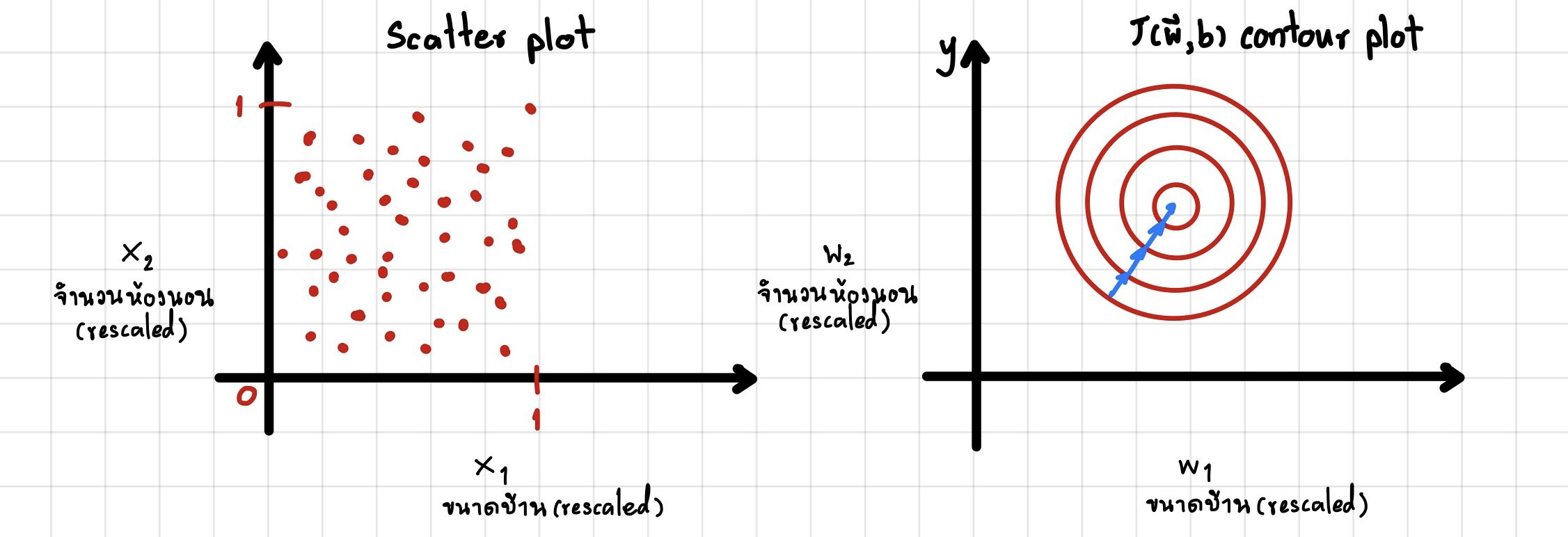
สามารถแก้ไขปัญหาข้างต้นได้โดยการทำ rescale
จากรูปเป็นการ rescaled x 1 , x 2 x_1,x_2 x 1 , x 2
วิธีที่กล่าวไปข้างต้นเรียกว่า Feature Engineering แบบ Feature Scaling
Feature Scaling วิธีการทำคือ หารค่าทั้งหมดของแต่ละ Feature ด้วยค่ามากสุดเช่น
300 ≤ x 1 ≤ 2000 x 1 , s c a l e d = x 1 2000 0.15 ≤ x 1 , s c a l e d ≤ 1 300 \leq x_1 \leq 2000 \\
x_{1,scaled} = \frac {x_1}{2000}\\
0.15 \leq x_{1,scaled} \leq 1 300 ≤ x 1 ≤ 2000 x 1 , sc a l e d = 2000 x 1 0.15 ≤ x 1 , sc a l e d ≤ 1 0 ≤ x 2 ≤ 5 x 2 , s c a l e d = x 2 5 0 ≤ x 2 , s c a l e d ≤ 1 0 \leq x_2 \leq 5 \\
x_{2,scaled} = \frac {x_2}{5}\\
0 \leq x_{2,scaled} \leq 1 0 ≤ x 2 ≤ 5 x 2 , sc a l e d = 5 x 2 0 ≤ x 2 , sc a l e d ≤ 1 Mean Normalization วิธีการทำคือ นำแต่ละค่าใน Feature มาลบด้วยค่าเฉลี่ยของ Feature และ หารด้วยค่า max - min ของ Feature
300 ≤ x 1 ≤ 2000 x 1 , s c a l e d = x 1 − μ 1 2000 − 300 − 0.18 ≤ x 1 , s c a l e d ≤ 0.822 300 \leq x_1 \leq 2000 \\
x_{1,scaled} = \frac {x_1 - \mu_{1}}{2000-300}\\
-0.18 \leq x_{1,scaled} \leq 0.822 300 ≤ x 1 ≤ 2000 x 1 , sc a l e d = 2000 − 300 x 1 − μ 1 − 0.18 ≤ x 1 , sc a l e d ≤ 0.822 0 ≤ x 2 ≤ 5 x 2 , s c a l e d = x 2 − μ 2 5 − 0 − 0.46 ≤ x 2 , s c a l e d ≤ 0.54 0 \leq x_2 \leq 5 \\
x_{2,scaled} = \frac {x_2-\mu_2}{5-0}\\
-0.46 \leq x_{2,scaled} \leq 0.54 0 ≤ x 2 ≤ 5 x 2 , sc a l e d = 5 − 0 x 2 − μ 2 − 0.46 ≤ x 2 , sc a l e d ≤ 0.54 Z-score Normalization วิธีการทำคือ นำแต่ละค่าใน Feature มาลบด้วยค่าเฉลี่ยของ Feature และ หารด้วยค่า SD ของ Feature
300 ≤ x 1 ≤ 2000 x 1 , s c a l e d = x 1 − μ 1 σ 1 − 0.67 ≤ x 1 , s c a l e d ≤ 0.31 300 \leq x_1 \leq 2000 \\
x_{1,scaled} = \frac {x_1 - \mu_{1}}{\sigma_1}\\
-0.67 \leq x_{1,scaled} \leq 0.31 300 ≤ x 1 ≤ 2000 x 1 , sc a l e d = σ 1 x 1 − μ 1 − 0.67 ≤ x 1 , sc a l e d ≤ 0.31 0 ≤ x 2 ≤ 5 x 2 , s c a l e d = x 2 − μ 2 σ 2 − 1.6 ≤ x 2 , s c a l e d ≤ 1.9 0 \leq x_2 \leq 5 \\
x_{2,scaled} = \frac {x_2-\mu_2}{\sigma_2}\\
-1.6\leq x_{2,scaled} \leq 1.9 0 ≤ x 2 ≤ 5 x 2 , sc a l e d = σ 2 x 2 − μ 2 − 1.6 ≤ x 2 , sc a l e d ≤ 1.9 แล้วเราต้องทำ Feature Scaling ตอนไหนบ้างล่ะ? ควรใช้ตอนที่ช่วง(range)ของ feature นั้นๆมีความกว้างเกินไปหรือแคบเกินไป ตัวอย่างเช่น
− 100 ≤ x ≤ 100 -100 ≤ x ≤ 100 − 100 ≤ x ≤ 100 แต่ถ้าช่วง(range)อยู่ในช่วงที่ยอมรับได้ไม่จำเป็นต้องทำ เช่น
− 1 ≤ x ≤ 1 − 3 ≤ x ≤ 3 − 0.3 ≤ x ≤ 0.3 0 ≤ x ≤ 3 − 2 ≤ x ≤ 0.5 \begin{aligned}
-1&≤x≤1\\
-3&≤x≤3\\
-0.3&≤x≤0.3\\
0&≤x≤3\\
-2&≤x≤0.5\\
\end{aligned} − 1 − 3 − 0.3 0 − 2 ≤ x ≤ 1 ≤ x ≤ 3 ≤ x ≤ 0.3 ≤ x ≤ 3 ≤ x ≤ 0.5 Feature Engineering ในบางครั้ง(จริงๆก็เกือบทุกครั้งนะ)การเลือก feature จะส่งผลกับความสามารถในการทำนายของ model ทั้งในทางที่ดีและไม่ดีและในบางครั้งเราก็ต้องมีการเล่นท่ายากกับ feature ที่มีอยู่เพื่อให้ได้มาซึ่ง feature ใหม่
เช่น การทำนายราคาบ้านโดยข้อมูลที่มีคือ
w i d t h : x 1 h e i g h t : x 2 \begin{aligned}
width &: x_1\\
height &: x_2\\
\end{aligned} w i d t h h e i g h t : x 1 : x 2 จะได้ Model เป็น
f ( x ) = w 1 x 1 + w 2 x 2 + b f(x) = w_1x_1 + w_2x_2 +b f ( x ) = w 1 x 1 + w 2 x 2 + b ด้วย feature เท่านี้อาจจะสามารถทำให้ Model สามารถทำนายราคาบ้านได้ดีในระดับนึงแล้วแต่เราสามารถทำให้มัน(อาจจะ)ดีขึ้นได้โดยการทำ Feature Engineering
จาก feature ที่มีอยู่ตอนนี้เราสามารถสร้้าง feature ใหม่ได้อีกตัวนั่นคือ
a r e a ( w i d t h × h e i g h t ) : x 3 area (width \times height): x_3 a re a ( w i d t h × h e i g h t ) : x 3 และเราจะได้ Model ใหม่คือ
f ( x ) = w 1 x 1 + w 2 x 2 + w 3 x 3 + b f(x) = w_1x_1 + w_2x_2+w_3x_3 +b f ( x ) = w 1 x 1 + w 2 x 2 + w 3 x 3 + b 💡
การจะทำ Feature Engineering ได้จะต้องมีความรู้ความเข้าใจในชุดข้อมูลนั้นๆ
จาก Feature Engineering ที่กล่าวไปข้างต้นในบางครั้งอาจจะทำให้ Model ของเราจากที่เป็น Linear Regression กลายเป็น
Polynomial Regression ในบางที่ข้อมูลของเราจะเมื่อนำไปทำ scatter plot แล้วจะมีแน้วโน้มที่ไม่ได้เป็น Linear การนำ Polynomial Regression มาใช้จะทำให้ Model เราสามารถ fit กับข้อมูลได้มากกว่า
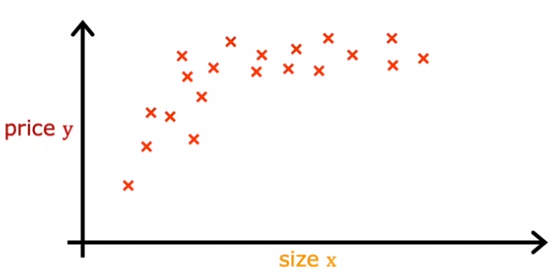
ตัวอย่าง scatter plot ของข้อมูลที่ไม่ได้มีแนวโน้มเป็นแบบ Linear ตัวอย่างเช่น ขนาดของบ้าน และ ราคาบ้าน สมมติว่าบ้านเป็นลูกบากศ์
ถ้าเราใช้ Model เป็น Linear Regression โดย ใช้แค่ความกว้าง
w i d t h : x 1 \begin{aligned}
width &: x_1\\
\end{aligned} w i d t h : x 1 Model ของเราจะเป็น
f ( x ) = w x + b f(x) = wx +b f ( x ) = w x + b แต่ถ้าเราเพิ่ม พื้นที่ และ ปริมาตรเข้าไปด้วยจะทำให้ Model ของเรากลายเป็น Polynomial Regression
จะได้ Model ใหม่เป็น
f ( x ) = w 1 x + w 2 x 2 + w 3 x 3 + b f(x) = w_1x + w_2x^2+w_3x^3 +b f ( x ) = w 1 x + w 2 x 2 + w 3 x 3 + b ซึ่ง(อาจ)จะสามารถ fit กับข้อมูลได้มากกว่าแบบแรก
Coming Soon …